Steinberg WaveLab для делающих самые первые шаги. Урок 1

Источник: "3DNews" Автор: Кристофер Дата: 24.10.2006

Я помню, как некогда «грыз гранит науки» в одном заведении, так там нас обучали компьютерам… в теории. Да-да, вот именно то, что многие сейчас и подумали. То есть, мы чертили в конспектах Norton Commander и так далее. Чтобы было более понятно, это все равно, что нарисовать на бумаге фортепианную клавиатуру и разучивать на ней фуги Баха, а потом сдавать по ним лабораторные на концертном рояле. В принципе, все так и выглядело. Именно поэтому у меня сейчас родилась идея не описывать программу по многочисленным просьбам читателей, и не делать очередной вводный материал для начинающих, а совместить все в одном. Причем, таким образом, мы исключим множество лишних вопросов, и, если нужно, возместим существующие пробелы.

Steinberg WaveLab – звуковой редактор №1 в мире. Профессиональная энциклопедия в виде программы. Думается, что этих эпитетов достаточно. Повествование будет о современном редактировании звука в целом, а WaveLab у нас выступит в качестве примера и опоры. Приступим…

Отображение звуковой волны. Основы номер 1

Как уже знают многие, цифровой сигнал является выборкой определенных значений из непрерывного аналогового. А для тех, кто не знает, поясню. Человек воспринимает информацию, а она передается за счет сигнала. Сигнал проявляется в изменении какого-либо параметра, любого. Как передается звук? В воздухе это изменения давления в среде, в электрическом токе — изменения напряжения и тока. Но мы воспринимаем все в непрерывном режиме, причем человека легко и обмануть. Вспомните кино с его 24 кадрами в секунду. Точно также решили сделать и в звуке, то есть выяснили с какой частотой нужно выбирать значения из непрерывного сигнала так, чтобы это не было заметно для человеческого уха. Это легло в теорию современного аудио, и, как факт, мы слушаем компакт-диски или МР3-файлы. Для того чтобы объяснить, что происходит в устройстве аналого-цифрового преобразователя можно и не мудрствовать особо. В каждый отсчет времени АЦП измеряет текущее напряжение в непрерывном аналоговом сигнале, сравнивает его с имеющейся шкалой своих напряжений и присваивает ближайшее подходящее. Таким образом, получается некая совокупность равномерно последовательно выбранных точек.

В результате, открыв в WaveLab любой звуковой файл (меню File —> Open —> Wave), вы и увидите результаты действия АЦП, а для большей информативности можете рассмотреть волну при самом крупном масштабе. Что вы увидите? Лесенку. Причем во многих других звуковых программах вместо нее точки выборки соединяются плавными линиями, но это не верно, поскольку между этими самыми точками никаких других значений и нет.

Для эксперимента вы можете на панели курсоров мыши выбрать режим карандаша, и попробовать нарисовать звуковую волну от руки, оставляя масштаб самым крупным. Что тогда произойдет? Редактор поведет себя как АЦП, то есть сделает выборку и присвоит свои ближайшие значения для точек, превращая нарисованную плавную линию в некое подобие лестницы. Количество выбранных значений за одну секунду называется частотой дискретизации (Sample Rate).

Сам редактор WaveLab устроен таким образом, что при максимальном масштабе он показывает посэмпловое (поточечное) разрешение при любых частотах дискретизации, но, в теории, если бы вы нарисовали карандашом одну и ту же линию для файлов с различными значениями этой характеристики, то количество «ступенек» в одном временном промежутке для каждого из случаев было бы различным. То есть, чем больше частота дискретизации, тем большим количеством выбранных значений вы оперируете. Но важно ли это? Вспомните пример с кино. Какая вам разница, 24 или 48 кадров будет воспроизводиться в секунду? И, в принципе, такое утверждение будет во многом верным, только вот в звуке есть один нюанс.

Помните, мы говорили, что АЦП сравнивает текущее значение непрерывного сигнала со своей шкалой значений? И что это за шкала такая? На самом деле, это просто двоичный код с определенным количеством разрядов (или бит). То есть, существует некий диапазон, именуемый динамическим, который может описываться определенным количеством значений. Например, в двухбитном варианте их будет 2 во второй степени (то есть, 4), в трехбитном — 2 в третьей (т.е., 8) и так далее. Чем больше разрядность (битность или Bitrate) преобразователя, тем больше точность его работы. И как раз эта цифровая характеристика является наиболее важной для описания качества цифрового звука. А частота дискретизации уже давно объяснена критериями Найквиста (теоремой Котельникова), и эту характеристику действительно нужно воспринимать, как и 24 кадра в кино (а в цифровом звуке распространен стандарт Красной Книги для аудио CD — 44,1 КГц). Именно поэтому во многих модулях обработки (плагинах) в качестве основного критерия указывается их разрядность, ведь в процессе работы появляется множество промежуточных значений, которые лучше учитывать, чем нет. Но при этом стоит отметить тот факт, что наилучшим вариантом является работа на повышенных величине разрядности и значении частоты дискретизации.

Отображение звуковой волны. Основы номер 2

Открыв звуковой файл в обычном режиме, вы смотрите на звук только с одной, даже можно сказать, однобокой стороны, то есть вам показаны текущие изменения значений уровня сигнала в процессе времени (это называется амплитудно-временным представлением). Стоит отметить, что в природе звук таков и есть. Но наши органы слуха и мозг ведут себя как призма, то есть расщепляют сложную звуковую волну на ряд простых. Кстати, первым такое предположение сделал известный физик Георг Ом еще в 1820 году, а само преобразование такого характера было придумано чуть раньше Жаном-Батистом Жозефом Фурье. Для чего вам это нужно знать? Практически все звуковые программы современности позволяют графически показать внутреннее частотное наполнение звуковых файлов, кои по существу хранят в себе сложные волны. Причем по сравнению с 19-м веком практически ничего не изменилось, разве что преобразования Фурье оптимизировали под цифровые вычислительные технологии.

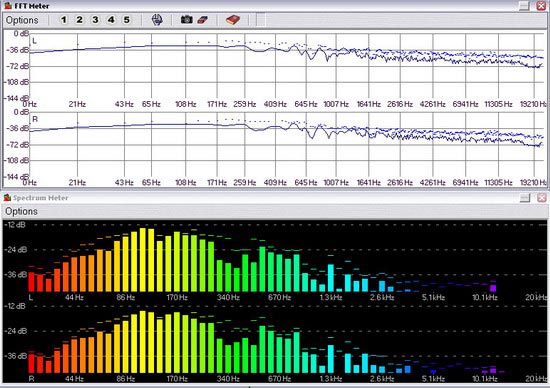
Для примера, запустите звуковой файл на воспроизведение и откройте индикатор FFT Meter (на панели горячих кнопок либо из меню Analysis —> Spectrum Analyser (FFT)). В процессе воспроизведения вы наглядно увидите, как работает алгоритм Быстрого Преобразования Фурье (FFT — Fast Furie Transform). Если объяснять его суть простыми словами, то в каждый определенный момент, из амплитудно-временного представления выбирается некоторое количество точек (фрагмент), из них формируется сложная периодическая функция, которая разбивается на ряд простых синусоидальных — получаем спектр. Длина этого фрагмента указывается заранее, и вы это можете увидеть, если зайдете в закладку Options —> Settings из окна данного индикатора. Оно (это количество) может быть как 512 точек, так и все 262144 (максимально предусмотрено программой). Причем, если на тех же 512 точках вам будет казаться, что индикатор работает в режиме реального времени, то на 262144 он будет менять изображение раз в три секунды на частоте дискретизации 44,1 КГц. Этот опыт вы можете проделать самостоятельно, а выводом из него будет являться то, что для Быстрого Преобразования Фурье необходимо иметь определенное количество точек в амплитудно-временном представлении, чтобы потом построить представление частотное.

А теперь посмотрите на другой схожий модуль, который в WaveLab называется Spectrum Meter (60 bands), а по существу является упрощенным вариантом FFT Meter. Структура преобразования сохранена практически та же, но при этом весь частотный спектр разбит на 60 полос. Точно такие же по сути, но менее профессиональные индикаторы вы можете увидеть в ряде пользовательских приложений, например, в WinAmp.

Отображение звуковой волны. Основы номер 3

Следующим этапом выделите некий фрагмент звукового файла, и вызовите пункт меню Analysis —> 3D Frequency Analysis. Перед вами откроется трехмерный график с осями: время, амплитуда, частота. Именно это и есть правильное понимание и представление звука в целом. Таким его видят и звукорежиссеры, и программисты профессионального софта.

Давайте посмотрим на этот график более внимательно. На самом деле он построен очень умно. Например, если вы присмотритесь к нему в цветном исполнении, то начиная от низких частот увидите «Каждый Охотник Желает Знать Где Сидит Фазан» (в переводе со школьной поговорки для запоминания — Красный, Оранжевый, Желтый, Зеленый, Голубой, Синий, Фиолетовый), то есть, обозначено подобие нашего цветового и слухового восприятий. И, на самом деле, зрение и слух у человека имеют очень много общего, а, если говорить прямо, то и в видео, и в аудио часто используются одни и те же технологии и алгоритмы, только названы они по-разному. Кстати, не так давно был выпущен словарь, объясняющий звуковые термины для видеоспециалистов на их языке. Но это мы немного отстранились от темы. Возвращаемся.

Часто у начинающих специалистов, особенно очень молодых, возникает простой и очевидный вопрос: а почему частотная шкала нелинейна. То есть на том же индикаторе FFT мы видим, что от 20 до 86 Гц занято столько же места, сколько и для диапазона от 2 до 14 КГц. Все дело в том, что так устроен наш слух. Данная шкала станет равномерной, если вы ее представите… хотя бы в виде фортепианной клавиатуры. А с физической точки зрения, то есть математическо-частотной, где измеряется количество колебаний в секунду, все выглядит неравномерно, но правильно с точки зрения слуха. Точно также и с амплитудным представлением звуковой волны (громкостью), ведь на самом деле, децибельная шкала основана на десятичных логарифмах, и введена она не спроста, поскольку тоже описывает ощущения человека.

Впрочем, вы в этом можете и сами убедиться, воспользовавшись тем, что в настройках данного 3D-графика можно произвести переключение частотной и амплитудной шкал в линейное либо логарифмическое представление. Это достаточно удобно с точки зрения информативности, а во-вторых, наглядно показывает разницу. Вашему вниманию представлены графики для одного и того же звукового фрагмента, но в различных представлениях шкал, если сверху вниз, то амплитуда линейна - частота логарифмическая, амплитуда логарифмическая – частота логарифмическая, амплитуда линейна – частота линейна:

В шестой версии WaveLab появилась новая возможность отображения звуковой волны в сонограммном виде. Чтобы глубоко не лезть и не отходить от темы, отметим, что сонограмма представляет собой двухмерный вид нашего 3D-графика сверху, а по осям получается частота и время. Но параллельно с этим за счет специального цветового распределения показана амплитуда, то есть третья ось (амплитуда) существует неявно. Это очень удобно, причем в WaveLab такая возможность вывода информации появилась запоздало, поскольку до этого уже использовалась в ряде программ типа Adobe Audition. Благодаря такому представлению достаточно легко находить «всплески» на тех или иных частотах, что в обычном амплитудно-временном виде вычисляется достаточно трудно, и, вообще-то, даже не видно.

Промежуточное завершение

В общем, любой гитарист вам может сказать, что начинать обучение лучше на дорогом инструменте, сделанном профессионалами. И звук лучше изучать не на дэнсмейкерах, где человек, ничего не понимая, двигает кирпичики с сэмплами, а на хороших качественных программах, в основе которых лежит профессиональный подход к делу. А теперь перейдем к теоретическим моментам и попытаемся ответить на вопрос…

Что такое громкость?

У многих начинающих специалистов возникают некоторые трудности с пониманием такой характеристики как «громкость». На самом деле в этом нет ничего сложного, и все что вам нужно — это внимательно прочесть эти пару абзацев…

Апельсины или килограммы?

В чем можно измерять, например, массу? Да, в принципе, во всем, чем угодно — хоть в килограммах, а хоть и в апельсинах. Ничего существенного от этого не поменяется, ведь мы можем перевести те же апельсины в килограммы и наоборот. Но если вы говорите, например, «10 апельсин» или «2,5 кг апельсин», что представляется более реальным в нашем воображении? Конечно, «10 апельсин».

А как быть с громкостью? Картина практически та же. В акустическом звуке мы можем оперировать такими стандартными физическими величинами, как интенсивность звуковой волны (пДж/м^2*с) или звуковым давлением (Н/м^2). При описании аналогового сигнала, можно без труда пользоваться теми же значениями уровня напряжения (В), силы тока (А) или мощности (Вт). То есть, они все подходят для описания уровня громкости, точно также как и килограммы в массе.

Но, возвращаясь к примеру с массой, в данном случае нам лучше «переходить на апельсины». Почему? Громкость — это субъективная величина, описывающая слуховые восприятия человека, то есть его ауральные ощущения. Изменив, например, значение интенсивности в 1000 раз, вы получите ощущение примерно 30-кратного увеличения громкости. Из-за чего это происходит? Потому как саму громкость мы воспринимаем нелинейно.

Поэтому ученые решили ввести промежуточные величины, которые просто являются более удобными в обращении и применении. Они связаны со стандартными физическими, но при этом более близки к описанию ощущений.

Переход к децибелам

Изначально громкость измерялась в «неперах», основанных на натуральных логарифмах, то есть 1 непер соответствует изменению уровня громкости в «е» - раз (е = 2.7). Но на практике гораздо удобнее использовать не натуральные логарифмы, а десятичные. Они проще в вычислениях. Так был и введен «Белл". 1 Белл — это очень крупная величина, и со временем в силу удобства стали широко использовать его 1/10-ю часть или «децибел» (дБ). Причем она оказалась достаточно удобной, поскольку соответствует нашему минимальному ощущению изменения уровня громкости. Хотя последнее утверждение не всегда верно, вы часто можете встретить, что чувствительность человеческого уха составляет 1-2 дБ. Вопрос в той же нелинейности (представьте себе график логарифма).

Формула!

Тут будет совсем немножко математики — объясним, чем так удобны децибелы, и как этим исчислением пользоваться.

В этом примере мы вообще не станем привязываться к чему-то конкретному (интенсивности, мощности и т.п.), взяв на вооружение обычную формулу N=10*lg(Х1/Х2) (дБ), где Х1 и Х2 — это два значения какой-либо величины. И поставим такое задание: параметр Х изменился в 100 раз, чему это будет равно в децибелах? Решение:

Если параметр увеличился в 100 раз, то все решается как N=10*lg(100)= 20 дБ. Если же параметр уменьшится в 100 раз, то мы получим N=10*lg(0,01)= -20 дБ. То есть, можно ответить, что изменение параметра в 100 раз соответствует изменению на 20 дБ. Причем, как вы можете увидеть, при Х1>Х2 мы получаем положительные значения в дБ, а при Х1<Х2 — отрицательные. Это очень важно понимать, поскольку очень часто у новичков возникает путаница со знаками. Сейчас мы развеем и ее.

Акустический звук

Как уже говорилось, в акустике мы оперируем такими величинами как интенсивность и звуковое давление. Мы их измеряем и вставляем в формулу по вычислению децибелов, но с чем сравниваем? На самом деле с нижним порогом слышимости, который соответствует 1 пДж/м^2*с (интенсивность) или же 0.000002 Н/м^2 (звуковое давление). То есть, априори, мы всегда сравниваем большее с меньшим, поэтому получаем только положительные значения в дБ. В отличие от приведенной в предыдущем примере формулы, числовой коэффициент в расчете силы звука по значениям звукового давления равен 20, а не десяти, а высчитанное таким образом значение в Дб обозначается, как дБ SPL.

Перед вами представлена стандартная таблица значений силы звука и наших ощущений. Благодаря ей вы поймете, почему так удобны децибелы. Ведь увеличение громкости на ту же величину в 100 Дб соответствует увеличению звукового давления в 100 000 раз, а интенсивности в 10^10 раз. Оперировать такими порядками чисел не всегда удобно (да и вообще не нужно). Например, что вам скажет значение звукового давления в 6.32*10^-4 Н/м^2? Ничего, а на самом деле это сила звука в 50 дБ.

Аналоговый и цифровой звук

А вот в аналоговом и цифровом звуке, мы в большинстве случаев будем оперировать отрицательными значениями в дБ. Это достаточно просто объяснимо — текущие (измеряемые) значения напряжения, силы тока или мощности мы сравниваем с опорными величинами, принятыми в телефонной связи, которые в свою очередь больше. То есть, если кому интересно, это Pоп = 1 мВт, Uоп = 0,775 B, I оп = 1,29 А. Причем мы имеем ряд других стандартов, в зависимости от чего, вы можете столкнуться с дополнительными обозначениями: если опорное напряжение равно 1 В — это dBV (наше дБв), а при 0,775 В — dBu (Дб) и dBm (дБм).

Данные величины описывают уровень сигнала и имеют вторичное отношение к нашему понятию «громкости», но в силу своей универсальности они более приемлемы для описания текущих процессов. Ведь здесь опять же изменение в 100 Дб будет соответствовать изменению мощности в 10^10 раз, или напряжения или тока в 10^5 раз.

На самом деле, все чуть сложнее

В принципе, использование такой величины как децибел не является спасением ото всех бед. Дело в том, что мы воспринимаем громкость неравномерно и по отношению к частотам. Например, научным путем выяснено, что наиболее громко мы слышим частоты 700 Гц-6 КГц, то есть в среднем частотном диапазоне. Это имеет прямое отношение к человеческой физиологии и окружающей нас природе. Кстати, большинство музыкальных инструментов, изобретенных человеком, имеет ключевой спектр как раз в указанном диапазоне — 700 Гц-6 КГц, там же находятся и наши голоса. Во-вторых, у каждой из характеристик звуковой волны измеряются ее пиковые, мгновенные и среднеквадратические значения. Последние являются наиболее важными для описания нашего ощущения громкости.

На этом все, продолжим в следующий раз …

Титул